Формула розрахунку очікуваних кредитних збитків ECL

Математика МСФЗ 9

Поняття очікуваних кредитних збитків (ECL) досить повно визначається відповідними положеннями МСФЗ 9 (5.5.17–5.5.20, B5.5.28–B5.5.35). Проте відомо, що будь-який текст, який регламентує розрахунки, завжди створює певну двозначність розуміння, якщо не містить формули розрахунку (звичайно, слід також пам’ятати про існування Gödel's incompleteness theorems).

Від стандартів, як документів найвищого рівня регламентування, надання формул ніколи не вимагалося. Тому при імплементації будь-якого «розрахункового» стандарту виникає задача правильного «перепрограмування» його вербальних вимог в діючі розрахункові моделі.

В стандартах технічного регулювання подібний «переклад» слів на формули відбувається майже автоматично, тому що їх термінологія співпадає з тією, що використовують профільні фахівці.

Скажімо, згадка в стандарті про «математичне сподівання» однозначно вказує на формулу, за якою його слід розрахувати. 

Саме тому розриву між вимогами стандарту та формулами, що їх на практиці реалізують, в стандартах з технічного регулювання не виникає.

На нашу думку, подібний «місточок» між словами в МСФЗ 9 і формулами для його застосування в Україні виявився вельми хитким.

Дійсно, ми досить часто спостерігаємо як чіткі «розрахункові» положення МСФЗ 9 трактуються деякими банківськими фахівцями, та навіть аудиторами-консультантами, занадто довільно.

На наш погляд, це відбувається тому, що залишається не поміченим цікавий факт – деякі ключові терміни МСФЗ 9 по суті відсилають до чітких «формульних» математичних визначень.

Саме це дозволяє однозначно «запрограмувати» вимоги МСФЗ 9 у формулах розрахунків очікуваних кредитних збитків (ECL).

Спробуємо розібратися в цьому питанні, принагідно збудувавши стрижень найпростішої математичної моделі для розрахунку ECL на lifetime основі.  

 Термінологія МСФЗ 9 вказує на певну математичну модель 

Розглянемо фінансові інструменти з наступними властивостями, що не обмежить загальність побудованої моделі:

• інструмент не містить позабалансових зобов’язань
• не передбачена модифікація без припинення визнання
• інструмент не є первинно знеціненим

Спочатку прочитаємо визначення очікуваних кредитних збитків (ECL) за українським текстом перекладу МСФЗ 9:

• "Б 5.5.28 Очікувані кредитні збитки – це зважена за ймовірністю оцінка кредитних збитків (тобто теперішня вартість усіх недоотриманих сум грошових коштів) за весь очікуваний строк дії фінансового інструмента..."

Дійсно, посилання на формулу дисконтування питань не викликає. Проте, з точки зору конструювання алгоритмів розрахунку ECL, основна невизначеність, на нашу думку, полягає у можливостях довільного трактування понять «імовірність» та «очікування». Використання у визначенні ECL математичного поняття «ймовірність» прямо вказує на необхідність звернутися до математичного визначення «очікування».

Аутентичний текст МСФЗ 9 на англійській мові використовує сталий термін “expected value” для математичного визначення поняття ECL.

Дійсно, процитуємо текст МСФЗ англійською мовою:

• "B 5.5.28 Expected credit losses are a probability-weighted estimate of credit losses (ie the present value of all cash shortfalls) over the expected life of the financial instrument...."

Зауважимо, що стандартом прямо регламентовано використання моделі дискретної випадкової величини для оцінювання ECL.

Порівняйте визначення МСФЗ 9 із дещо спрощеним математичним визначенням:

• за IFRS 9: “B 5.5.28 Expected credit losses are a probability-weighted estimate of credit losses (ie the present value of all cash shortfalls) over the expected life of the financial instrument”, а ось
• «словесне» математичне визначення: “The expected value of a discrete random variable is the probability-weighted average of all possible values”.

Найпростіша математична модель, яка регламентована МСФЗ 9

Для скінченної множини реалізацій вимога стандарту щодо формули для ECL може бути записана наступним чином.

Нехай X випадкова величина грошового потоку від фінансового інструмента зі скінченним набором реалізацій х_i, що відбуваються з імовірністю p_i

• "5.5.17 Суб'єкт господарювання оцінює очікувані кредитні збитки за фінансовим інструментом у спосіб, що відображає: (а) об'єктивну та зважену за ймовірністю суму, визначену шляхом оцінки певного діапазону можливих результатів…".

Тоді очікуване значення грошового потоку від фінансового інструмента X визначається з урахуванням умови розгляду повної групи подій (сума всіх імовірностей має дорівнювати одиниці) наступним чином:

Просуваємося далі, щоб «перепрограмувати» у формули наступні вимоги стандарту:

• "5.5.18 При оцінці очікуваних кредитних збитків суб'єкт господарювання може не визначати всі можливі сценарії. Водночас, він має врахувати ризик або ймовірність настання кредитних збитків шляхом розгляду можливості настання кредитного збитку та можливості ненастання кредитного збитку, навіть якщо можливість настання кредитного збитку є малоймовірною"
• "Б5.5.41 ... оцінка очікуваних кредитних збитків завжди має відображати можливість настання кредитних збитків і можливість ненастання кредитних збитків, навіть якщо найімовірнішим результатом є ненастання кредитних збитків».

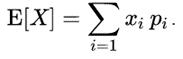
Підкреслимо, що розглядається найпростіша модель з кінцевою кількістю подій. 

З урахуванням цих вимог стандарту, наведена вище формула приводить, як мінімум, до найпростішої моделі дефолту:

• «подія дефолту в періоді t відбувається з імовірністю PD_t  або
• «дефолт в періоді t не стався», звісно, з імовірністю 1 - PD_t,

Влив на ECL майбутніх економічних умов

В моделі потрібно врахувати не тільки положення (а) п. 5.5.17 стандарту:

• "Суб'єкт господарювання оцінює очікувані кредитні збитки за фінансовим інструментом у спосіб, що відображає: (а) об'єктивну та зважену за ймовірністю суму, визначену шляхом оцінки певного діапазону можливих результатів…" –

а й відповідний п. (в):

• "Суб'єкт господарювання оцінює очікувані кредитні збитки за фінансовим інструментом у спосіб, що відображає: (в) … прогнози майбутніх економічних умов…станом на звітну дату".

Для цього слід вважати PD_t функціями не тільки часу, а й «прогнозів майбутніх економічних умов» (5.5.17). 

Цього можна досягти, скажімо, заданням певних макроекономічних сценаріїв із ймовірностями настання p_s, де s – номер сценарію.

Ймовірності настання сценаріїв, а також кількість таких сценаріїв, на нашу думку, слід визначити розрахунковими методами.

Припустимо, що все це зроблено, тоді позначимо:

• CCF_t – контрактний грошовий потік періоду t,
• PD_ts – ймовірність дефолту протягом періоду за певним «прогнозом майбутніх економічних умов… станом на звітну дату» (5.5.17), що визначений сценарієм s,
• EAD_t-1 – кредитна експозиція на початку періоду,
• PV_ts – приведена на кінець періоду справедлива вартість грошового потоку від застав та інших забезпечень з урахуванням трансакційних витрат на їх реалізацію. Відповідно до положення стандарту (Б5.5.55) щодо врахування потоків від застав, доречно вважати приведену вартість PV_ts також залежною від "прогнозу майбутніх економічних умов…" (5.5.17), тобто від макроекономічних сценаріїв.

За таких умов очікувана величина потоку за фінансовим інструментом протягом одного часового інтервалу t буде визначатися наступною формулою:

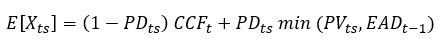
Cтруктуровані грошові потоки на основі Lifetime

Повернемося до визначення і згадаємо, що ми розглядаємо lifetime основу, для якої стандарт вимагає врахування «усіх можливих подій дефолту за весь очікуваний строк дії фінансового інструмента» (додаток А до стандарту). У прямому визначені також наголошується:

• "Б 5.5.28 Очікувані кредитні збитки – це зважена за ймовірністю оцінка кредитних збитків … за весь очікуваний строк дії фінансового інструмента."

Вказані вимоги відображаємо у формулах, враховуючи, що будь-яка подія в певному періоді може статися тільки в разі, якщо до цього дефолт ще не відбувся.

Тобто боржник всі попередні періоди до t «прожив» без дефолту, що описується функцією S_st-1. Функція S_st-1, звичайно, залежить від імовірностей дефолту в кожному з періодів, що передують періоду t, та має задовольняти вимогам повноти групи подій у нашій імовірнісній моделі.

Вивчення фактичних властивостей S_st-1 зручно здійснювати досить поширеними статистичними методами, що об’єднані загальним класом Survival analysis. Ми також здійснюємо аналіз за допомогою всіх методів цього класу.

В результаті отримаємо очікуваний потік з урахуванням «дожиття»:

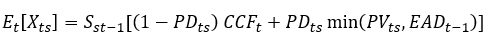
 Останній акорд

Для завершення процесу створення формули будемо використовувати наступні положення стандарту:

• "Б5.5.29 У випадку фінансових активів кредитним збитком є теперішня вартість різниці між: (а) договірними грошовими потоками, належними до сплати на користь суб'єкта господарювання за договором; і (б) грошовими потоками, які суб'єкт господарювання очікує одержати",
• "5.5.17 Суб'єкт господарювання оцінює очікувані кредитні збитки за фінансовим інструментом у спосіб, що відображає:

• (а) об'єктивну та зважену за ймовірністю суму, визначену шляхом оцінки певного діапазону можливих результатів;
• (б) часову вартість грошей і; 
• (в) обґрунтовано необхідну та підтверджувану інформацію про минулі події, поточні умови та прогнози майбутніх економічних умов, яка може бути одержана без надмірних витрат або зусиль станом на звітну дату".

Це надає підстави записати остаточний результат наступним чином у припущенні, що r – ефективна ставка в момент первинного визнання:

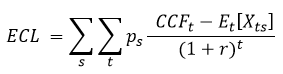
Деякі можливі узагальнення

Отримана нами формула, звичайно, не враховує деякі особливості розрахунку ECL для певних інструментів.

Скажімо, випадок імовірної модифікації без припинення визнання інструмента, наявність пов’язаних зобов’язань (кредитна лінія) тощо.

Для інструментів з елементами пов’язаних зобов’язань і безвідкличних позабалансових зобов’язань (гарантії, непокриті акредитиви тощо) формулу безпосередньо використовувати неможна. Це пов’язано з необхідністю розбудови більш складної моделі, яка має враховувати прогноз щодо використання інструментів таких типів. Проте запропонований нами підхід досить легко застосувати для розрахунку ECL за фінансовими інструментами з можливостями модифікації без припинення їх визнання. 

Для виведення формули ECL із врахуванням модифікації інструмента пропонуємо скористатися наступною схемою, де p – ймовірність модифікації.

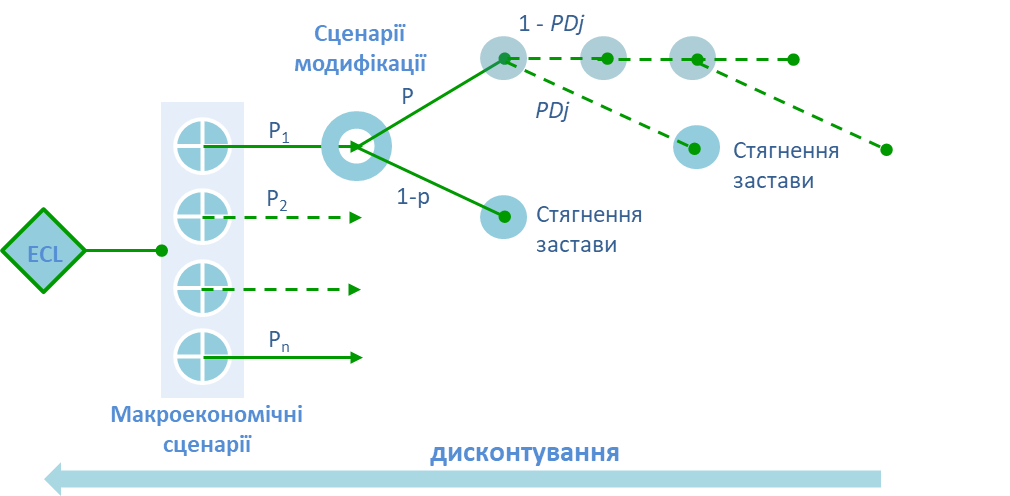
Модельна формула, яку ми побудували вище, демонструє практично всі аспекти розбудови більш складних моделей розрахунку ECL, що узагальнено в наступній принциповій схемі.